
Bài 2: Định Lí Đảo Và Hệ Quả Của Định Lí Ta-lét
I. Định lý talet đảo
1. Định lý đảo
Định lý talet đảo: Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác. (SGK, trang 60)
2. Ví dụ:
Ví dụ 1: Quan sát hình sau và cho biết DE có song song với BC không? Vì sao?
Giải:
Ta có: ;
Xét tam giác ABC có:
( Định lý talet đảo)
Ví dụ 2: Quan sát hình bên. Tứ giác BDEF là hình gì? Vì sao?
Giải:
Ta có: ;
Xét tam giác ABC có:
( Định lý talet đảo) hay DE // BF
Ta có : ;
Xét tam giác ABC có:
(Định lý talet đảo) hay EF // BD
Xét tứ giác BDEF có (cmt)
⇒ Tứ giác BDEF là hình bình hành.
II. Hệ quả của định lý talet
1. Hệ quả của định lý talet
Nếu một đường thẳng cắt hai cạnh của một tam giác và song song với cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho. (SGK, trang 60)
Chứng minh:
Xét tam giác ABC có B’C’ // BC (định lý talet) (1)
Kẻ C’D song song với AB.
Khi đó tứ giác BB’C’D có C’D// BB’; B’C’// BD nên tứ giác BB’C’D là hình bình hành.
Xét tam giác ABC có C’D // AB (định lý talet)
( B’C’ = BD) (2)
Từ (1) (2) suy ra ( đpcm)
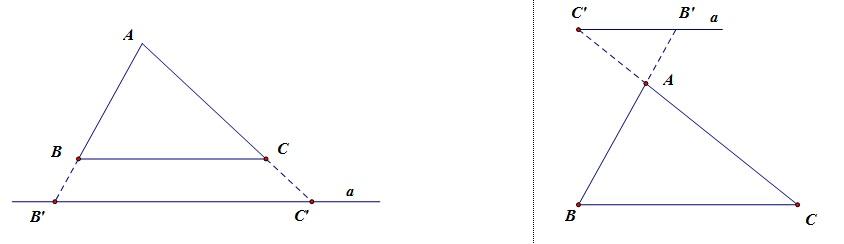
Lưu ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại (h.11): (SGK, trang 61)
2. Ví dụ.
a) Tìm x trong hình bên, biết DE // BC.
Giải:
AB = AD + DB = 2 + 3 = 5 cm
Xét tam giác ABC có (gt)
(hệ quả của định lý talet)
Vậy x = 6,25 cm
b) Tìm x trong hình bên:
Giải
Xét tam giác MNP có: (gt)
( hệ quả của định lý talet)
Vậy x = 3cm.
Giáo viên biên soạn: Trần Thị Kim Duyên (Trường THCS - THPT Nguyễn Khuyến BD)
Link nội dung: https://sgk.edu.vn/he-qua-cua-dinh-ly-talet-a70979.html