
Lý thuyết Một số bài toán về tỉ số và tỉ số phần trăm Toán 6 KNTT với cuộc sống
I. Tỉ số
a) Tỉ số của hai số
Chú ý: Nếu tỉ số của $ a$ và $ b$ được viết dưới dạng $ dfrac{a}{b}$ thì ta cũng gọi $ a$ là tử số và $ b$ là mẫu số.
Ví dụ:
Tỉ số của $ - 5$ và $ 7$ là: $ dfrac{{ - 5}}{7}$ .
b) Tỉ số của hai đại lượng
Nhận xét:
Tỉ số của hai đại lượng thể hiện độ lớn của đại lượng này so với đại lượng kia.
Chú ý:
- Phân số $ dfrac{a}{b}$ thì cả $ a$ và $ b$ phải là các số nguyên.
- Tỉ số $ dfrac{a}{b}$ thì $ a$ và $ b$ có thể là các số nguyên, phân số, hỗn số, số thập phân,…
Ví dụ:
Tỉ số chiều dài hai đoạn thẳng $ AB = 1,5,,,cm$ và $ CD = dfrac{1}{3},cm$ là: $ 1,5:dfrac{1}{3}$ .
II. Tỉ số phần trăm
Ví dụ:
a) Tỉ số phần trăm của $ 3$ và $ 6$ là:
$ dfrac{{3.100}}{6}% = dfrac{{300}}{6}% = 50% .$
b) Tỉ số phần trăm của $ - 2,3$ và $ 10$ là: $ dfrac{{ - 2,3.100}}{{10}}% = - 23% $
Chú ý: Tỉ số $ dfrac{{a.100}}{b}$ không nhất thiết là số nguyên.
III. Tìm giá trị phần trăm của một số
Ví dụ:
$99,99% $ của $3,75$ là: $3,75.dfrac{{99,99}}{{100}} = 3,749625$
IV. Tìm một số khi biết giá trị phần trăm của số đó
Ví dụ:
Số có giá trị $2,5% $ bằng $200$ là số: $200:dfrac{{2,5}}{{100}} = 8,000$
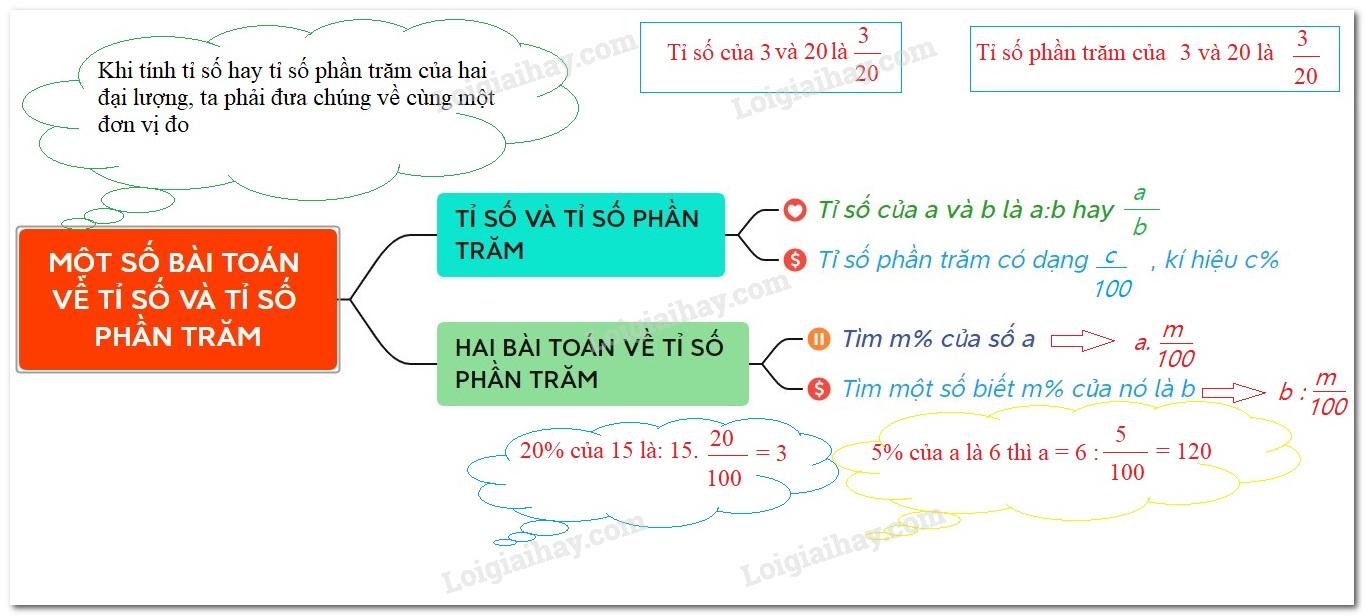
CÁC DẠNG TOÁN VỀ TỈ SỐ VÀ TỈ SỐ PHẦN TRĂM
I. Tính tỉ số của hai số
Để tính tỉ số của hai số ta tính $ a:b$ hoặc $ dfrac{a}{b}$ $ left( {b ne 0} right)$
II. Tính tỉ số phần trăm của hai đại lượng
Để tính tỉ số phần trăm của a và b, ta làm như sau:
Bước 1. Viết tỉ số $ dfrac{a}{b}$
Bước 2. Tính số $ dfrac{{a.100}}{b}$ và viết thêm % vào bên phải số vừa nhận được.
III. Viết các số thập phân, phân số dưới dạng tỉ số phần trăm và ngược lại
- Viết một số a dưới dạng dùng kí hiệu %: (a = dfrac{{a.100}}{{100}} = (100.a)% )
- Viết (a% ) dưới dạng phân số: (a% = dfrac{a}{{100}})
- Đổi số thập phân ra phân số: (overline {a,bc} = dfrac{{overline {abc} }}{{100}} = overline {abc} % ;,,,,,overline {a,{b_1}{b_2}...{b_n}} = dfrac{{a{b_1}{b_2}...{b_n}}}{{{{10}^n}}})
- Một phân số tối giản có mẫu số chỉ có ước số nguyên tố là 2 hoặc 5 thì có thể viết dưới dạng số thập phân (hữu hạn).
IV. Sử dụng tỉ số phần trăm trong thực tế
Tỉ số phần trăm thường được sử dụng trong đời sống để giải quyết một số bài toán như:- Mua bán hàng ngày
- Lãi suất tín dụng
- Thành phần các chất hóa học.
Link nội dung: https://sgk.edu.vn/tinh-ti-so-a70551.html