Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 Giải SGK Toán 10 trang 65 - Tập 1 sách Chân trời sáng tạo

Toán 10 Chân trời sáng tạo trang 65 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Thực hành và 7 bài tập được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Chân trời sáng tạo trang 65 tập 1 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 Chân trời sáng tạo trang 65 mời các bạn cùng theo dõi.

Phần Thực hành Toán 10 Chân trời sáng tạo Bài 1

Thực hành 1

Tìm các giá trị lượng giác của góc 135 0

Gợi ý đáp án

Hình vẽ minh họa:

Lấy điểm A trên nửa đường tròn đơn vị sao cho 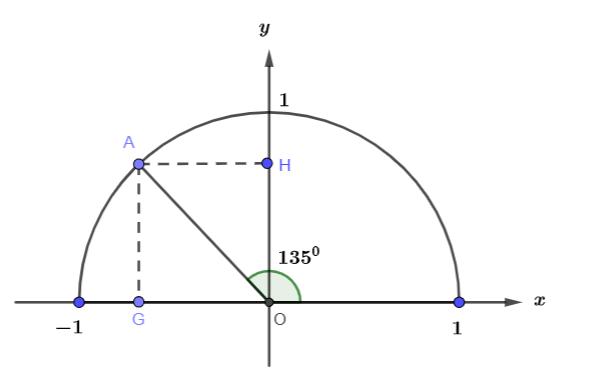(widehat {xOA} = {135^{0}})

Ta có:

(widehat {yOA} = {180^0} - {135^0} = {45^0})

Ta tính được tọa độ điểm A là 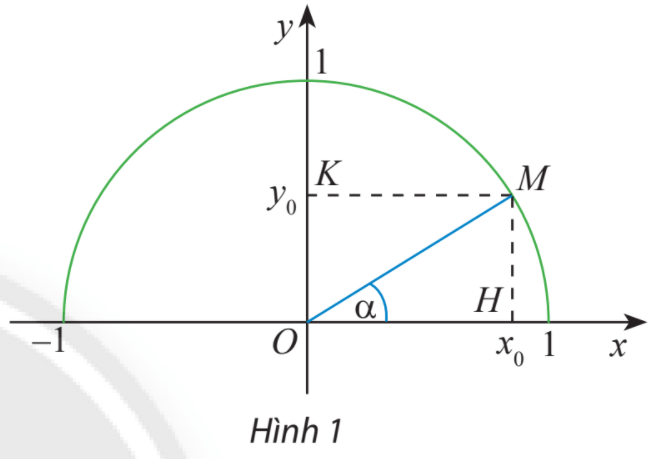(A = left( {frac{{ - sqrt 2 }}{2};frac{{sqrt 2 }}{2}} right))

Vậy theo định nghĩa ta có:

(sin {135^0} = frac{{sqrt 2 }}{2})

(cos{135^0} = -frac{{sqrt 2 }}{2})

(tan {135^0} =- 1)

(cot {135^0} = -1)

Thực hành 2

Tính các giá trị lượng giác sin120 0 ; cos150 0 ; cot135 0 .

Gợi ý đáp án

Thực hiện phép tính ta có kết quả như sau:

sin1200 = sin (1800 - 1200) = sin600 = (frac{{sqrt 3 }}{2})

cos1500 = -cos(1800 - 1500) = -cos 300 = (-frac{{sqrt 3 }}{2})

cot1350 = - cot(1800 - 1350) = -cot 450 = -1

Bài tập Toán 10 trang 65 Chân trời sáng tạo

Bài 1 trang 65 Toán 10 Chân trời sáng tạo

Cho biết (sin {30^o} = frac{1}{2};sin {60^o} = frac{{sqrt 3 }}{2};tan {45^o} = 1). Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của

(E = 2cos {30^o} + sin {150^o} + tan {135^o}.)

Gợi ý đáp án

Ta có:

(begin{array}{l}cos {30^o} = sin left( {{{90}^o} - {{30}^o}} right) = sin {60^o} = frac{{sqrt 3 }}{2};sin {150^o} = sin left( {{{180}^o} - {{150}^o}} right) = sin {30^o} = frac{1}{2};tan {135^o} = - tan left( {{{180}^o} - {{135}^o}} right) = - tan {45^o} = - 1end{array})

(Rightarrow E = 2.frac{{sqrt 3 }}{2} + frac{1}{2} - 1 = sqrt 3 - frac{1}{2}.)

Bài 2 trang 65 Toán 10 Chân trời sáng tạo

Chứng minh các hệ thức sau:

(a) sin {20^o} = sin {160^o})

(b) cos {50^o} = - cos {130^o})

Gợi ý đáp án

a)

(sin {20^o} = sin left( {{{180}^o} - {{160}^o}} right) = sin {160^o})

b)

(cos {50^o} = cos ;({180^o} - {130^o}) = - cos {130^o})

Bài 3 trang 65 Toán 10 Chân trời sáng tạo

Tìm góc (alpha ;;({0^o} le alpha le {180^o})) trong mỗi trường hợp sau:

(a) cos alpha = - frac{{sqrt 2 }}{2})

(b) sin alpha = 0)

(c) tan alpha = 1)

d) (cot alpha) không xác định.

Gợi ý đáp án

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng (cos alpha)ta có:

(cos alpha = frac{{ - sqrt 2 }}{2} với alpha = {135^o})

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng (sin alpha)ta có:

(sin alpha = 0 với alpha = {0^o} và alpha = {180^o})

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng (tan alpha)ta có:

(tan alpha = 1 với alpha = {45^o})

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng (cot alpha)ta có:

(cot alpha)không xác định với (alpha = {0^o})

Bài 4 trang 65 Toán 10 Chân trời sáng tạo

Cho tam giác ABC. Chứng minh rằng:

(a) sin A = sin ;(B + C))

(b) cos A = - cos ;(B + C))

Gợi ý đáp án

a)

(sin (B + C) = sin left( {{{180}^o} - A} right) = sin A)

Vậy (sin A = sin ;(B + C))

b)

(cos (B + C) = cos left( {{{180}^o} - A} right) = - cos A)

Vậy (cos A = - cos ;(B + C))

Bài 5 trang 65 Toán 10 Chân trời sáng tạo

Chứng minh rằng với mọi góc (alpha ;;({0^o} le alpha le {180^o}),) ta đều có:

Gợi ý đáp án

(a) {cos ^2}alpha + {sin ^2}alpha = 1)

Trên nửa đường tròn đơn vị, lấy điểm M sao cho (widehat {xOM} = alpha)

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

Ta có: tam giác vuông OHM vuông tại H và (alpha = widehat {xOM})

Do đó: (sin alpha = frac{{MH}}{{OM}} = MH;;cos alpha = frac{{OH}}{{OM}} = OH.)

(Rightarrow {cos ^2}alpha + {sin ^2}alpha = O{H^2} + M{H^2} = O{M^2} = 1)

b) (tan alpha .cot alpha = 1;({0^o} < alpha < {180^o},alpha ne {90^o}))

Ta có:

(begin{array}{l};tan alpha = frac{{sin alpha }}{{cos alpha }};;cot alpha = frac{{cos alpha }}{{sin alpha }}. Rightarrow ;tan alpha .cot alpha = frac{{sin alpha }}{{cos alpha }}.frac{{cos alpha }}{{sin alpha }} = 1end{array})

(c) 1 + {tan ^2}alpha = frac{1}{{{{cos }^2}alpha }};(alpha ne {90^o}))

Với (alpha ne {90^o}) ta có:

(begin{array}{l};tan alpha = frac{{sin alpha }}{{cos alpha }};; Rightarrow ;1 + {tan ^2}alpha = 1 + frac{{{{sin }^2}alpha }}{{{{cos }^2}alpha }} = frac{{{{sin }^2}alpha + {{cos }^2}alpha }}{{{{cos }^2}alpha }} = frac{1}{{{{cos }^2}alpha }};end{array})

(d) 1 + {cot ^2}alpha = frac{1}{{{{sin }^2}alpha }};({0^o} < alpha < {180^o}))

Ta có:

(begin{array}{l}cot alpha = frac{{cos alpha }}{{sin alpha }};; Rightarrow ;1 + {cot ^2}alpha = 1 + frac{{{{cos }^2}alpha }}{{{{sin }^2}alpha }} = frac{{{{sin }^2}alpha + {{cos }^2}alpha }}{{{{sin }^2}alpha }} = frac{1}{{{{sin }^2}alpha }};end{array})

Bài 6 trang 65 Toán 10 Chân trời sáng tạo

Cho góc (alpha) với (cos alpha = - frac{{sqrt 2 }}{2}). Tính giá trị của biểu thức (A = 2{sin ^2}alpha + 5{cos ^2}alpha .)

Gợi ý đáp án

Ta có: (A = 2{sin ^2}alpha + 5{cos ^2}alpha = 2({sin ^2}alpha + {cos ^2}alpha ) + 3{cos ^2}alpha)

Mà ({cos ^2}alpha + {sin ^2}alpha = 1;cos alpha = - frac{{sqrt 2 }}{2}.)

(Rightarrow A = 2 + 3.{left( { - frac{{sqrt 2 }}{2}} right)^2} = 2 + 3.frac{1}{2} = frac{7}{2}.)

Bài 7 trang 65 Toán 10 Chân trời sáng tạo

Dùng máy tính cầm tay, hãy thực hiện các yên cầu dưới đây:

a) Tính (sin {168^o}45'33'';cos {17^o}22'35'';tan {156^o}26'39'';cot {56^o}36'42''.)

b) Tìm (alpha ;({0^o} le alpha le {180^o})),trong các trường hợp sau:

(i) sin alpha = 0,862.)

(ii) cos alpha = - 0,567.)

(iii) tan alpha = 0,334.)

Gợi ý đáp án

a)

(begin{array}{l}sin {168^o}45'33'' = 0,195;cos {17^o}22'35'' = 0,954;tan {156^o}26'39'' = - 0,436;cot {56^o}36'42'' = 0,659end{array})

b)

(i) alpha = {59^o}32'30,8''.)

(ii) alpha = {124^o}32'28,65''.)

(iii) alpha = {18^o}28'9,55''.)