
50 bài tập về Quy tắc đếm (có đáp án 2024) và cách giải
Quy tắc đếm và cách giải các dạng bài tập - Toán lớp 11
1. Lý thuyết
a) Quy tắc cộng
* Định nghĩa:
Giả sử một công việc A được thực hiện theo k phương án khác nhau.
Phương án A1 có m1 cách thực hiện;
Phương án A2 có m2 cách thực hiện;
…
Phương án Ak có mk cách thực hiện;
Và mỗi phương án Ai không trùng với bất kì cách thực hiện các phương án Aj (với j≠i; i,j∈1;2;...;k)
Thì có m1 + m2 + … + mk cách thực hiện A.
* Công thức quy tắc cộng:
Nếu A1; A2; … ; Ak đôi một rời nhau. Khi đó
A1∪A2∪...∪Ak=A1+A2+...+Ak
Với |Ai| là số phần tử của tập hợp Ai (với i∈1;2;...;k)
A1∪A2∪...∪Ak là số phần tử của tập hợp A1∪A2∪...∪Ak.
b) Quy tắc nhân
Giả sử một công việc A được thực hiện theo k công đoạn liên tiếp.
Công đoạn A1 có m1 cách thực hiện;
Công đoạn A2 có m2 cách thực hiện;
…
Công đoạn Ak có mk cách thực hiện;
Thì có m1.m2. … mk cách thực hiện A.
* Công thức quy tắc nhân:
Nếu A1; A2; … ; Ak đôi một rời nhau. Khi đó
A1∩A2∩...∩Ak=A1.A2....Ak
Với |Ai| là số phần tử của tập hợp Ai (với i∈1;2;...;k)
A1∩A2∩...∩Ak là số phần tử của tập hợp A1∩A2∩...∩Ak.
c) Cách đếm
* Đếm trực tiếp:
- Chia các trường hợp có thể xảy ra
- Đếm số phương án thực hiện trong các trường hợp
- Kết quả của bài toán đếm là tổng số phương án đếm được trong các trường hợp trên.
* Đếm gián tiếp (Đếm phần bù): Dùng khi thực hiện công viêc phải chia nhiều trường hợp.
2. Các dạng bài tập
Dạng 1: Bài toán đếm số tự nhiên
Phương pháp giải:
* Lập số tự nhiên thỏa mãn điều kiện:
- Gọi số tự nhiên có ba chữ số là abc¯ với a,b,c∈ℕ; 1≤a≤9; 0≤b,c≤9.
Gọi số tự nhiên có bốn chữ số là abcd¯ với a,b,c,d∈ℕ; 1≤a≤9; 0≤b,c,d≤9.
Tương tự với số có hai, năm, sáu,… chữ số.
- Chọn chữ số có điều kiện trước, chữ số không có điều kiện sau (Chẳng hạn chọn chữ số a trước vì có điều kiện a≠0. Ở bài toán đếm số chẵn, lẻ, chia hết cho 2, 5, 10 thì đếm chữ số hàng đơn vị trước)
- Dùng quy tắc cộng, nhân để đếm số cần lập.
* Phân biệt cách dùng quy tắc cộng và quy tắc nhân:
- Quy tắc cộng: Một công việc có thể thực hiện được theo các phương án khác nhau, xảy ra phương án 1 thì sẽ không xảy ra phương án 2.
- Quy tắc nhân: Một công việc được hoàn thành khi phải thực hiện liên tiếp các công đoạn.
* Một số dấu hiệu khi lập số
- Dấu hiệu chia hết cho 2: Chữ số tận cùng là 0; 2; 4; 6; 8.
- Dấu hiệu chia hết cho 5: Chữ số tận cùng là 0; 5.
- Dấu hiệu chia hết cho 3: Tổng các chữ số chia hết cho 3.
- Dấu hiệu chia hết cho 9: Tổng các chữ số chia hết cho 9.
- Dấu hiệu chia hết cho 4: Hai chữa số tận cùng chia hết cho 4.
- Dấu hiệu chia hết cho 6: Chia hết cho cả 2 và 3.
- Số tự nhiên chẵn: Chữ số tận cùng là 0; 2; 4; 6; 8.
- Số tự nhiên lẻ: Chữ số tận cùng là 1; 3; 5; 7; 9.
Ví dụ minh họa:
Ví dụ 1. Từ các số A = {1; 2; 3; 4; 5; 6; 7}; có thể lập được bao nhiêu số tự nhiên thỏa mãn:
a) Số gồm 5 chữ số.
b) Số gồm 5 chữ số khác nhau.
c) Số gồm 5 chữ số khác nhau và chia hết cho 2.
d) Số gồm 5 chữ số lớn hơn 60000.
e) Số gồm 5 chữ số khác nhau, chứa chữ số 2 và chia hết cho 2.
Lời giải
Gọi số có 5 chữ số cần lập là abcde¯ với a,b,c,d,e∈1;2;3;4;5;6;7.
a) Số gồm 5 chữ số
Chọn a: có 7 cách chọn
Chọn b: có 7 cách chọn
Chọn c: có 7 cách chọn
Chọn d: có 7 cách chọn
Chọn e: có 7 cách chọn
Vậy có 75 số.
b) Số gồm 5 chữ số khác nhau.
Chọn a từ tập A: có 7 cách chọn
Chọn b từ tập A{a} (có 6 phần tử): có 6 cách chọn
Chọn c từ tập A{a; b} (có 5 phần tử): có 5 cách chọn
Chọn d từ tập A{a; b; c} (có 4 phần tử): có 4 cách chọn
Chọn e từ tập A{a; b; c; d} (có 4 phần tử): có 3 cách chọn
Vậy có 7.6.5.4.3 = 2520 số.
c) Số gồm 5 chữ số khác nhau và chia hết cho 2
abcde¯ chia hết cho 2 nên e∈2;4;6
Chọn e: có 3 cách chọn
Chọn a từ tập A{e} (có 6 phần tử): có 6 cách chọn
Chọn b từ tập A{e; a} (có 5 phần tử): có 5 cách chọn
Chọn c từ tập A{e; a; b} (có 4 phần tử): có 4 cách chọn
Chọn d từ tập A{e; a; b; c} (có 3 phần tử): có 3 cách chọn
Vậy có 3.6.5.4.3 = 1080 số.
d) Số gồm 5 chữ số lớn hơn 60000.
Vì abcde¯>60000
Nên a∈6;7. Chọn a: có 2 cách chọn
Chọn b từ tập A{a} (có 6 phần tử): có 6 cách chọn
Chọn c từ tập A{a; b} (có 5 phần tử): có 5 cách chọn
Chọn d từ tập A{a; b; c} (có 4 phần tử): có 4 cách chọn
Chọn e từ tập A{a; b; c; d} (có 4 phần tử): có 3 cách chọn
Vậy có 2.6.5.4.3 = 720 số.
e) Số gồm 5 chữ số khác nhau, chứa chữ số 2 và chia hết cho 2.
+ Số có 5 chữ số khác nhau và chia hết cho 2 có 1080 số (câu c)
+ Ta lập số có 5 chữ số khác nhau, chia hết cho 2 và không chứa chữ số 2:
abcde¯ chia hết cho 2 và không chứa 2 nên e∈4;6
Chọn e: có 2 cách chọn
Chọn a từ tập A{2; e} (có 5 phần tử): có 5 cách chọn
Chọn b từ tập A{2; e; a} (có 4 phần tử): có 4 cách chọn
Chọn c từ tập A{2; e; a; b} (có 3 phần tử): có 3 cách chọn
Chọn d từ tập A{2; e; a; b; c} (có 2 phần tử): có 2 cách chọn
Như vậy có 2.5.4.3.2 = 240 số có 5 chữ số khác nhau, chia hết cho 2 và không chứa chữ số 2.
Vậy có 1080 - 240 = 840 số có 5 chữ số khác nhau, chia hết cho 2 và chứa chữ số 2.
Ví dụ 2: Từ các số 0; 1; 2; 3; 4; 5 có thể lập được bao nhiêu số tự nhiên thỏa mãn:
a) Số lẻ có 5 chữ số khác nhau
b) Số có 5 chữ số khác nhau và chia hết cho 5
Lời giải
a) Gọi số có 5 chữ số cần lập là abcde¯ với a≠0, các chữ số được lấy từ A = {0; 1; 2; 3; 4; 5}.
abcde¯ là số lẻ nên e∈1;3;5. Chọn e: có 3 cách chọn
Chọn a từ tập A{0; e} (có 4 phần tử): có 4 cách chọn
Chọn b từ tập A{e; a} (có 4 phần tử): có 4 cách chọn
Chọn c từ tập A{e; a; b} (có 3 phần tử): có 3 cách chọn
Chọn d từ tập A{e; a; b; c} (có 2 phần tử): có 2 cách chọn
Vậy có 3.4.4.3.2 = 288 số lẻ có 5 chữ số khác nhau.
b) Gọi số có 5 chữ số cần lập là abcde¯ với a≠0, các chữ số được lấy từ A = {0; 1; 2; 3; 4; 5}.
abcde¯ chia hết cho 5 nên e∈0;5
+ Trương hợp 1: e = 0
Chọn a từ tập A{0} (có 5 phần tử): có 5 cách chọn
Chọn b từ tập A{0; a} (có 4 phần tử): có 4 cách chọn
Chọn c từ tập A{0; a; b} (có 3 phần tử): có 3 cách chọn
Chọn d từ tập A{0; a; b; c} (có 2 phần tử): có 2 cách chọn
Như vậy có 5.4.3.2 = 120 số.
+ Trường hợp 2: e = 5
Chọn a từ tập A{0; 5} (có 4 phần tử): có 4 cách chọn
Chọn b từ tập A{5; a} (có 4 phần tử): có 4 cách chọn
Chọn c từ tập A{5; a; b} (có 3 phần tử): có 3 cách chọn
Chọn d từ tập A{5; a; b; c} (có 2 phần tử): có 2 cách chọn
Như vậy có 4.4.3.2 = 96 số.
Vậy có tất cả 120 + 96 = 216 số có 5 chữ số khác nhau và chia hết cho 5.
Dạng 2: Bài toán đếm trong thực tế, phân công công việc
Phương pháp giải:
Sử dụng quy tắc cộng và quy tắc nhân.
Ví dụ minh họa:
Ví dụ 1. Từ thành phố A đến thành phố B có 3 con đường, từ thành phố B đến thành phố C có 4 con đường. Có bao nhiêu cách đi từ thành phố A đến thành phố C, biết phải đi qua thành phố B.
Lời giải
Cách 1: Làm bằng cách liệt kê các con đường đi:
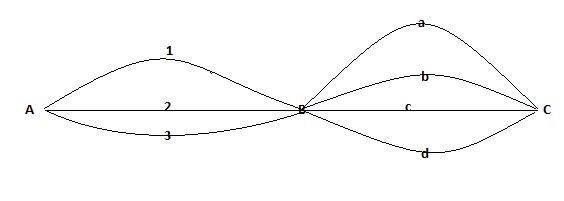
Căn cứ vào sơ đồ trên, ta có các con đường đi là: 1a, 1b, 1c, 1d, 2a, 2b, 2c, 2d, 3a, 3b, 3c, 3d. Vậy có 12 con đường.
Cách 2: Sử dụng quy tắc nhân
Đi từ A đến B có 3 con đường
Đi từ B đến C có 4 con đường
Vậy để đi từ A đến C có 3.4 = 12 con đường.
Ví dụ 2: Trong một lớp có 18 học sinh nam và 12 học sinh nữ. Hỏi có bao nhiêu cách chọn
a) Một bạn phụ trách lớp trưởng?
b) Hai bạn, trong đó có 1 bạn nam và 1 bạn nữ?
Lời giải
a) Chọn 1 bạn phụ trách lớp trưởng
Trường hợp 1: Chọn 1 bạn nam: có 18 cách chọn
Trường hợp 2: Chọn 1 bạn nữ: có 12 cách chọn
Vậy có 18 + 12 cách chọn.
b) Chọn 2 bạn, trong đó có 1 bạn nam và một bạn nữ
Chọn 1 bạn nam: có 18 cách chọn
Chọn 1 bạn nữ: có 12 cách chọn
Vậy có 18.12 = 216 cách chọn.
Dạng 3: Bài toán hình học
Phương pháp giải:
* Sử dụng quy tắc cộng và quy tắc nhân
* Chú ý:
- Đếm vectơ: Hai điểm đầu và cuối khác nhau (Tức là vectơ AB và vectơ BA tính 2 lần đếm khác nhau).
- Đếm đoạn thẳng: Hai đầu mút có vai trò như nhau (Tức là đoạn thẳng AB và đoạn thẳng BA chỉ tính 1 lần đếm)
Ví dụ minh họa:
Ví dụ 1. Cho hai đường thẳng song song d, d’. Trên d lấy 10 điểm phân biệt, trên d’ lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà đỉnh của nó được chọn từ 25 đỉnh nói trên?
A. 1050
B. 675
C. 1725
D. 708750
Lời giải
Chọn C
+ Trường hợp 1: Chọn 2 điểm từ d và 1 điểm từ d’
Chọn điểm thứ nhất từ d: có 10 cách chọn
Chọn điểm thứ hai từ d: có 9 cách chọn
Vì thay đổi thứ tự lấy điểm không tạo ra cách chọn mới nên số cách chọn 2 điểm từ đường thẳng d là 9.102=45 cách chọn.
Chọn 1 điểm từ d’: có 15 cách chọn
Như vậy có 45.15 = 675 cách chọn tam giác từ 2 điểm thuộc d và 1 điểm thuộc d’.
+ Trường hợp 2: Chọn 2 điểm từ d’ và 1 điểm từ d
Chọn điểm thứ nhất từ d’: có 15 cách chọn
Chọn điểm thứ hai từ d’: có 14 cách chọn
Vì thay đổi thứ tự lấy điểm không tạo ra cách chọn mới nên số cách chọn 2 điểm từ đường thẳng d’ là 15.142=105 cách chọn.
Chọn 1 điểm từ d: có 10 cách chọn.
Như vậy có 105.10 = 1050 cách chọn tam giác từ 2 điểm thuộc d’ và 1 điểm thuộc d.
Vậy có 675 + 1050 = 1725 tam giác được tạo ra.
Ví dụ 2. Trong mặt phẳng có 30 điểm. Có bao nhiêu vectơ khác vectơ - không mà điểm đầu và điểm cuối được lấy từ 30 điểm trên?
A. 870
B. 435
C. 302
D. 230
Lời giải
Chọn A
Chọn điểm đầu: có 30 cách chọn
Chọn điểm cuối: có 29 cách chọn
Vậy có 30.29 = 870 vectơ được lấy từ 30 điểm.
3. Bài tập tự luyện
Câu 1. Cho 6 chữ số 2; 3; 4; 5; 6; 7. Hỏi có bao nhiêu số gồm 3 chữ số được lập thành từ 6 chữ số đó?
A. 36
B. 18
C. 256
D. 216
Câu 2. Cho các số 1; 5; 6; 7. Có thể lập được bao nhiêu số tự nhiên có 4 chữ số với các chữ số khác nhau?
A. 12
B. 24
C. 64
D. 256
Câu 3. Số các số gồm 5 chữ số khác nhau chia hết cho 10 là
A. 3260
B. 3024
C. 5436
D. 12070
Câu 4. Từ các chữ số 0; 1; 2; 3; 4; 5 có thể lập được bao nhiêu số lẻ gồm 4 chữ số khác nhau?
A. 154
B. 145
C. 144
D. 155
Câu 5. Một người muốn chọn 1 bộ quần áo. Biết người đó có 5 cái quần và 4 cái áo sơ mi. Hỏi người đó có bao nhiêu cách chọn.
A. 9
B. 5
C. 4
D. 20
Câu 6. Từ các chữ số 0; 1; 2; 3; 4; 5; 6, lập được bao nhiêu số có hai chữ số khác nhau chia hết cho 3?
A. 10
B. 18
C. 12
D. 27
Câu 7. Từ các chữ số 0; 1; 2; 3; 4; 5; 6; 7, có thể lập được bao nhiêu số có ba chữ số khác nhau chứa chữ số 2 và chia hết cho 5?
A. 20
B. 21
C. 22
D. 23
Câu 8. Trong một trường THPT, khối 11 có 280 học sinh nam và 325 học sinh nữ. Nhà trường cần chọn hai học sinh trong đó có một nam và một nữ đi dự trại hè của học sinh thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
A. 910 000
B. 91 000
C. 910
D. 605
Câu 9. Một đội học sinh giỏi của trường THPT, gồm 5 học sinh khối 12, 4 học sinh khối 11, 3 học sinh khối 10. Số cách chọn ba học sinh trong đó mỗi khối có một em?
A. 12
B. 220
C. 60
D. 3
Câu 10. Có bao nhiêu cách sắp xếp 3 nữ sinh, 3 nam sinh thành một hàng dọc sao cho các bạn nam và nữ ngồi xen kẽ?
A. 6
B. 72
C. 720
D. 144
Câu 11. An muốn qua nhà Bình để cùng Bình đến chơi nhà Cường. Từ nhà An đến nhà Bình có 4 con đường đi, từ nhà Bình tới nhà Cường có 6 con đường đi. Hỏi An có bao nhiêu cách chọn đường đi đến nhà Cường?
A. 6
B. 4
C. 10
D. 24
Câu 12. Trong một hộp bóng, có 6 quả bóng xanh được đánh số từ 1 đến 6 và 4 quả bóng vàng được đánh số từ 7 đếm 10. Có bao nhiêu cách chọn một quả cầu trong hộp?
A. 24
B. 10
C. 6
D. 4
Câu 13. Có 3 bông hoa hồng, 4 bông hoa cúc, 5 bông hoa ly. Hỏi có bao nhiêu cách chọn 3 bông hoa sao cho có đủ 3 loại hoa?
A. 60
B. 12
C. 20
D. 15
Câu 14. Cho hai đường thẳng song song d, d’. Trên d lấy 15 điểm phân biệt, trên d’ lấy 12 điểm phân biệt. Hỏi có bao nhiêu tam giác mà đỉnh của nó được chọn từ 27 đỉnh nói trên?
A. 4860
B. 2250
C. 4500
D. 729
Câu 15. Trong mặt phẳng có 20 điểm, trong đó không có ba điểm nào thẳng hàng. Có đoạn thẳng mà 2 đầu mút được lấy từ 20 điểm trên?
A. 190
B. 380
C. 202
D. 220
Bảng đáp án
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
D
B
B
C
D
C
D
B
C
B
D
B
A
B
A
Xem thêm các dạng bài tập Toán lớp 9 có đáp án và lời giải chi tiết khác:
Hoán vị, Chỉnh hợp, Tổ hợp và cách giải các dạng bài tập
Nhị thức Niu-tơn và cách giải các dạng bài tập
Cách giải phương trình, bất phương trình tổ hợp chi tiết nhất
Xác định biến cố và tính xác suất của biến cố chi tiết nhất
Trọn bộ công thức tính xác suất đầy đủ, chi tiết nhất
Link nội dung: https://sgk.edu.vn/bai-tap-ve-quy-tac-dem-a69363.html